Nechci si hrát na experta na matematiku ani na experta na její didaktiku, na to jsou tu povolanější. Ale 3D grafika se nedá dělat bez trochy teorie z matematiky a geometrie. Nebudu zabíhat do nějakých šíleně formálních definic, protože je stejně neumím a nadělal bych tam spoustu chyb, a navíc by nikomu nic neřekly. Pokusím se jednoduše a prakticky vysvětlit, co jsou a jak se používají goniometrické funkce, a jak se pracuje s vektory v 3D prostoru. Hodně věcí budu zjednodušovat, aby se to vešlo do tohoto článku, ale nemělo by to být na úkor srozumitelnosti. Určitě v zájmu zjednodušení nezmíním různé krajní případy a dopustím se mnoha nepřesností, prosím znalé matematiky, aby mi prominuli. Cílem tohoto článku je vysvětlit začátečníkům, kteří ještě potřebné matematické znalosti nemají, alespoň základy této problematiky, minimální množinu věcí, které budeme potřebovat.
Goniometrické funkce anebo trocha teorie na začátek
Jistě je ze školních lavic dobře znáte, jedná se o funkce sinus, kosinus a tangens (ještě byly nějaké další, ale nám budou stačit tyto). Na základních školách se s těmito funkcemi pracuje ve stupních, ale daleko praktičtější je pracovat v radiánech, pojďme se na ně podívat.
Stupňová a oblouková míra
Všichni víme, že pravý úhel je 90 stupňů, plný úhel je pak 360 stupňů. Kromě stupňové míry máme také míru obloukovou, neboli úhel můžeme určit v radiánech. Máme-li kruhovou výseč (část koláče), kde poloměr má stejnou délku jako oblouk na kraji, pak má úhel u středu velikost právě 1 radián. Pro lepší představu máme obrázek:
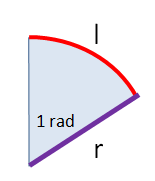
l je délka oblouku, r je poloměr. Pokud je úhel 1 radián, pak l = r. Ze školy si určitě pamatujete vzorec pro obvod kružnice, platí, že o = 2.π.r. Když jako kruhovou výseč vezmeme celou kružnici, pak oblouk je 2π krát delší než poloměr, takže plný úhel 360 stupňů = 2π radiánů. Předpokládám, že všichni víte, co je to π; pro jistotu, kdyby tady byl někdo mladší, kdo ho ještě ve škole neměl - π (pí) je Ludolfovo číslo a má hodnotu přibližně 3,14159. Je to poměr mezi obvodem kružnice a jejím průměrem.
Jak tedy převádět stupně a radiány mezi sebou? Je to jednoduchá trojčlenka (zkusíme převést 1 radián na stupně):
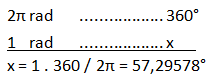
V XNA máme pro převádění stupňů a radiánů nachystané metody MathHelper.ToDegrees a MathHelper.ToRadians, které převádí radiány na stupně, resp. stupně na radiány.
Sinus
Nyní se podíváme na funkci sinus. Tato funkce má periodu 2π, základní interval je [0, 2π]. Její graf jistě všichni znáte, vypadá takto:
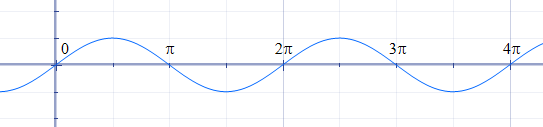
V bodě π/2 má funkce hodnotu 1, v bodě 3π/2 má hodnotu -1. Od 2π dále se její základní interval neustále opakuje-
Kosinus
Kosinus je mírně posunutý sinus, opět je 2π periodický a základní interval je [0, 2π]. Graf této funkce vypadá takto:
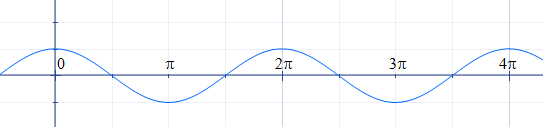
V bodě 0 má funkce hodnotu 1, v bodě π má funkce hodnotu -1. Od 2π dále se její základní interval také neustále opakuje.
Jednotková kružnice
Hodnoty funkcí sin a cos se dají najít také na tzv. jednotkové kružnici. Dejme tomu, že chceme zjistit hodnoty funkcí sin a cos v bodě π/6 (30 stupňů). Nakreslíme si tedy kružnici o poloměru 1 a naneseme si na ní požadovaný úhel. Hodnoty funkce sin a cos budou vzdálenosti průsečíku polopřímky a kružnice od vodorovné, resp. svislé osy procházející středem kružnice:
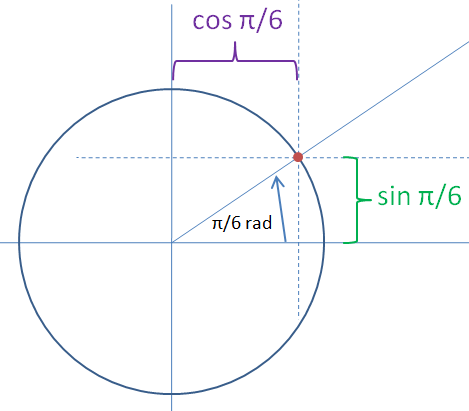
Poloměr kružnice musí být 1, aby hodnoty funkcí sin a cos vyšly. Úhel se nanáší od vodorovné osy ve směru šipky. Všimněte si, že pokud nanesete úhel 0, hodnota funkce sin bude 0 a funkce cos jakoby 1, červená tečka se nám posune po kružnici na osu X doprava. Vzdálenost od vodorovné osy bude 0 a vzdálenost od svislé 1. Takže vidíme, že to vychází. Když bude tečka pod vodorovnou osou, resp. vlevo od svislé osy, musíme vzít vzdálenost záporně, aby to vyšlo.
Tangens
Funkci tangens vezmu jen tak, aby se neřeklo. Ve skutečnosti platí tan(x) = sin(x) / cos(x), tam, kde je cos(x) = 0 funkce tangens není definována. Funkce tangens má periodu π, její základní interval je [-π/2, π/2]. Vypadá takto:
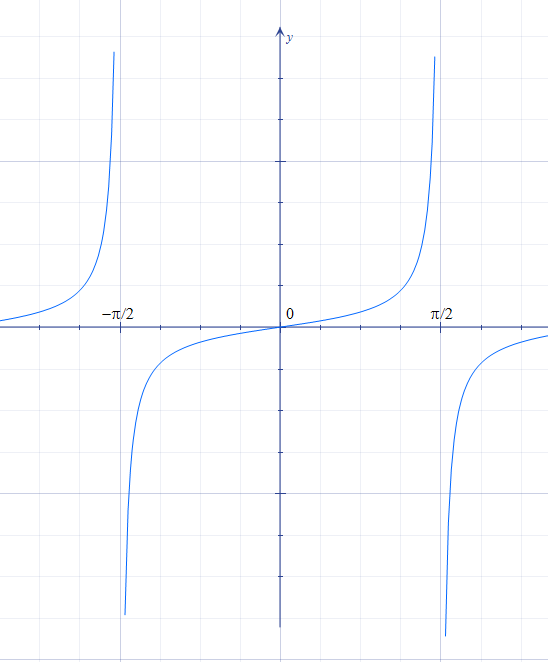
V bodech -π/2 a π/2 jdou hodnoty funkce k ∞ zleva a k -∞ zprava. Od π/2 se stále opakuje základní interval funkce.
Pravoúhlý trojúhelník
Máme-li pravoúhlý trojúhelník, pomocí goniometrických funkcí můžeme vyjádřit vztahy mezi délkami stran a velikostmi úhlů:
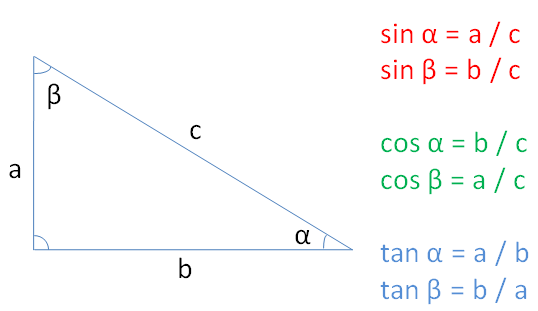
Tím bychom mohli s goniometrickými funkcemi skončit. Předpokládám, že jste je všichni znali, ale pro připomenutí se to hodí. Zvlášť uvědomit si jednotkovou kružnici je velice důležité, budeme ji potřebovat a vlastně jsme ji již v minulých dílech použili, akorát jsem se o tom nezmiňoval.
Trocha 3D geometrie ještě nikoho nezabila
V některém z minulých dílů jsme si už povídali o vektorech a souřadnicích. Nyní si zde jen v rychlosti projdeme základní operace s vektory. Pak si řekneme něco o reprezentaci ploch v 3D prostoru, protože se nám to určitě někdy příště bude hodit.
Vektor
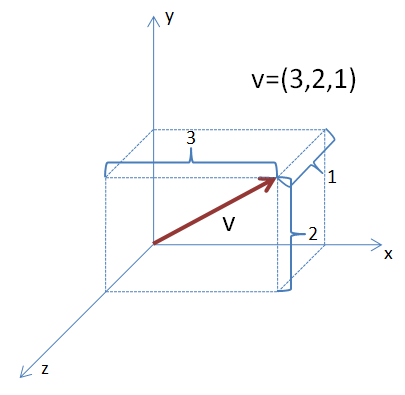
Vektor nám ve 3D prostoru určuje vzdálenost a směr. S vektorem můžeme provádět několik operací:
Vynásobení vektoru číslem
Nechť v je vektor a a je číslo, pak vektor a.v má stejný směr, změní se pouze jeho délka. Pokud je a záporné, směr vektoru se přeci jen změní, bude ukazovat přesně na druhou stranu. Pokud v = (x, y, z), pak a.v = (a.x, a.y, a.z). Každá složka vektoru se vynásobí číslem a.
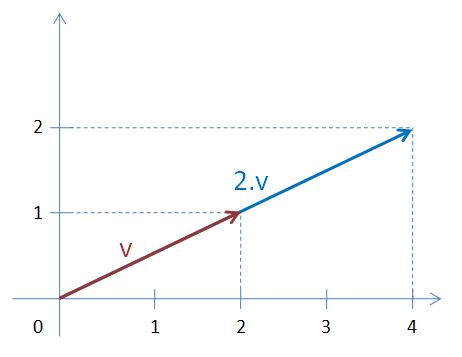
Na tomto obrázu (ve 2D, ale to je jedno), vidíme vektor v=(2,1) a vektor 2.v, jehož souřadnice jsou vynásobené dvěmi, tzn. 2.v=(4,2). Je snadné nahlédnout, že délka vektoru se také zdvojnásobila.
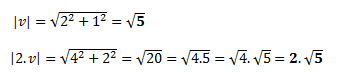
Dá se to samozřejmě vyjádřit i obecně, aby bylo jasné, že to platí pro každé velikosti souřadnic vektorů, dvojka na druhou se ve druhém výrazu pod odmocninou vytkne, a pak se odmocní. Pro výpočet délky vektoru jsme použili známou Pythagorovu větu. Pro trojsložkové vektory to bude to samé, akorát že pod odmocninou budou všechny tři souřadnice:
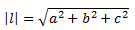a, b, c jsou jednotlivé souřadnice vektoru
Pokud vektor vynásobíme číslem záporným, obrátí se jeho směr. Opačný vektor k v je -v, má souřadnice (-2,-1).
Dva vektory v a w jsou rovnoběžné, pokud existuje číslo k tak, že v = k . w, jinak řečeno pokud jeden vektor je násobkem vektoru druhého.
Součet vektorů
Nechť v a w jsou dva vektory a v = (a, b) a w = (c, d). Pak v + w = (a+c, b+d) a vypadá to takto:
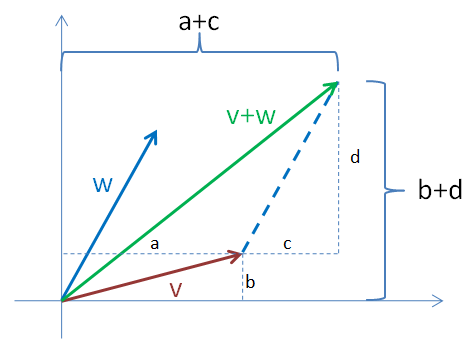
Pokud vektor w posuneme tak, aby začínal tam, kde vektor v končí, získáme jednu polovinu rovnoběžníka. Úhlopříčkou tohoto rovnoběžníka je pak vektor v+w. Z obrázku je vidět, že souřadnice zeleného vektoru opravdu vychází jako součty souřadnic x a y vektorů v a w.
Nemá smysl zvlášť rozebírat odčítání vektorů, je to to samé, jako sčítání vektoru v s vektorem -w, který už umíme sestrojit. Opět vyjde nějaký rovnoběžník a součet (rozdíl) vektorů bude úhlopříčka na něm. Samozřejmě to funguje i ve 3D prostoru, akorát už nemáme rovnoběžník, ale jakýsi "rovnoběžnostěn".
Skalární součin vektorů
Nechť v a w jsou opět dva vektory, pak skalárním součinem je číslo z, které vznikne vynásobením souřadnic po složkách a jejich sečtením. Nechť v=(a, b, c) a w=(d, e, f), pak z = <v | w> = a . d + b . e + c . f. Výraz <v | w> čteme jako skalární součin vektorů v a w.
Skalární součin vektorů můžeme použít k vypočítání mnoha užitečných informací, například pomocí něj můžeme zjistit, jaký mezi sebou vektory svírají úhel. Pokud jsou vektory u a v normalizované (mají délku 1), pak cos a = <u | v>, kde a je úhel, který mezi sebou tyto vektory svírají.
Pokud se skalární součin dvou vektorů rovná nule, jsou na sebe vektory kolmé. Opět platí jak v rovině, tak i ve 3D prostoru.
Vektorový součin
Nechť v a w jsou opět dva vektory (nerovnoběžné), pak vektorový součin v × w je vektor, který je kolmý jak na vektor v, tak i na vektor w. Tady už jasně vyplývá, že tohle funguje pouze ve 3D prostoru, protože jeden vektor nemůže být v rovině kolmý na dva různoběžné vektory. V prostoru je to naproti tomu velmi užitečné.
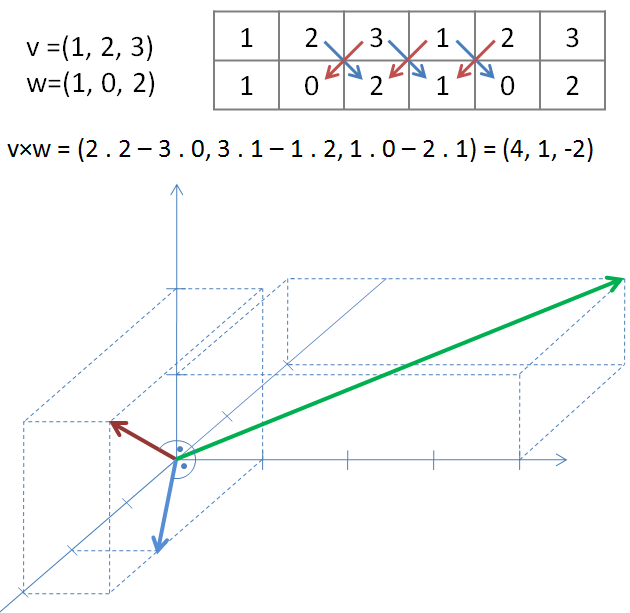
Jak se součin počítá? Souřadnice vektorů v a w si zapíšeme do tabulky, zopakujeme je postupně dvakrát za sebe, čili v každém řádku máme x y z x y z. Pak po směru šipek počítáme jednotlivé souřadnice. Modrá šipka značí, že součin čísel přičítáme, červená znamená, že součin odčítáme. První kříž je první souřadnice, druhý kříž je druhá a třetí kříž je třetí souřadnice.
První souřadnici součinu tedy získáme ze součinů 2 . 2 (modrá šipka) a 3 . 0 (červená šipka). První součin přičteme, druhý odečteme, takže první souřadnice je + 2 . 2 - 3 . 0, tedy 4. Obdobně vypočítáme další dvě souřadnice.
Na obrázku jsem nakreslil vektory v a w (červený a modrý). Vektor v×w je dlouhý zelený vektor. Obrázek není úplně přesný, 3D prostor je zkreslený použitou projekcí, takže úhly také nemůžeme měřit úhloměrem, nemají skutečné velikosti. Pokud ale máte trochu prostorové představivosti, vidíte, že zelený vektor je kolmý jak na vektor červený, tak na vektor modrý.
Je nutno podotknout, že v×w není to samé co w×v, na pořadí vektorů v tomto součinu záleží. Pokud bychom vzali vektorový součin w×v, dostaneme jako výsledek vektor opačný, tzn. zelený vektor by měl stejnou délku, ale vedl by na opačnou stranu. Vyplývá to ze způsobu, jak vektorový součin počítáme, když prohodíme řádky tabulky, tak dvojice, které se přičítaly, se budou odčítat, a naopak. Dostaneme tedy opačné souřadnice.
Přímka v prostoru
Přímka obecně je určena jedním bodem a jedním vektorem. Vektor udává pouze směr, nikoliv už pozici, kde se nachátí. Proto potřebujeme nějaký bod, aby bylo jasné, kudy přímka prochází, a směr už určí vektor. To platí jak v rovině, tak i v prostoru.
Přímku v prostoru i v rovině můžeme vyjádřit parametricky:
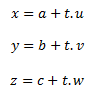
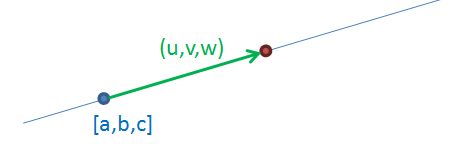
Přímka na obrázku je zadána modrým bodem se souřadnicemi a,b,c a zeleným vektorem se souřadnicemi u,v,w. Parametrické vyjádření přímky jsou tři rovnice vedle obrázku. Pokud za a,b,c a u,v,w dosadíme, pak pro každé číslo, které dosadíme za t nám vyjdou x,y,z souřadnice nějakého bodu, který leží na přímce. Proč? Protože číslem t násobíme vektor, čímž měníme pouze jeho délku, nikoliv směr. Pomocí čísla t jsme tedy schopni "ukázat vektorem" na každý bod přímky, včetně toho modrého (za t dosadíme nulu) i bodů, které jsou na opačné straně (t dosadíme záporné).
A naopak pokud nám někdo zadá bod a chceme zjistit, jestli leží na naší přímce, zkusíme k němu najít číslo t. Známe modrý bod i vektor a souřadnice bodu x,y,z, o kterém zjišťujeme, jestli na přímce je, máme tedy 3 rovnice s jednou neznámou, což není problém spočítat. Pokud nám ve všech řádcích vyjde stejné t, pak bod na přímce leží. V opačném případě je bod x,y,z mimo přímku, protože nemůžeme zelený vektor natáhnout po přímce tak, aby dosáhl na bod x,y,z. Museli bychom změnit jeho směr, což už ale nejde, protože ho můžeme jen vynásobit číslem.
Rovina v prostoru
S rovinou je to velmi podobné jako s přímkou, je zadána jedním bodem a dvěma vektory, které nesmí být rovnoběžné (protože tím by nám rovina nevznikla, oba vektory musí začínat v daném bodě, jinak to nemá smysl; pozor - vektor není přímka!).
Rovinu můžeme také vyjádřit parametricky:
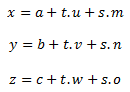
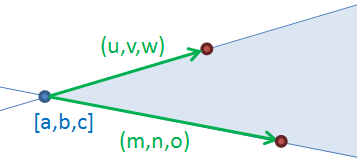
Opět pomocí kombinace čísel t a s můžeme "ukázat" na libovolný bod roviny a pokud chceme zjistit, jestli bod x,y,z v rovině leží, dosadíme do rovnic a řešíme soustavu. V případě, že najdeme právě jedno řešení, tzn. všechny rovnice budou platit pro jedno konkrétní t a jedno konkrétní s, pak bod x,y,z v rovině leží.
Rovina se dá také zadat pomocí bodu a normálového vektoru. O normále jsme se již bavili v některém z minulých dílů, normála je přímka, která je kolmá na nějakou rovinu. Normálový vektor bude tedy vektor kolmý na tuto rovinu:
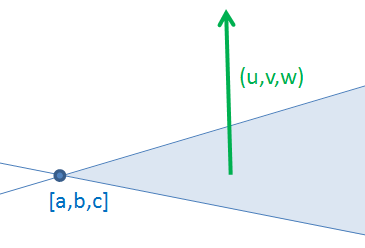
Na těchto ilustracích je rovina omezena přímkami, ve skutečnosti je každá rovina, stejně jako přímka nekonečná, stejně jako máme nekonečně mnoho možností pro volbu t, resp. t a s. Tady, aby bylo něco vidět, máme rovinu ohraničenou a bledě modře znázorněnou její část.
V praxi se místo modrého bodu používá konstanta c, což je vzdálenost roviny od počátku vzhledem k délce normálového vektoru. Pokud rovina prochází počátkem, je c nula. Vzhledem k tomu, že jako vzdálenost bodu a roviny se bere vzdálenost nejkratší možná, která vede po kolmici, je to vlastně délka měřená ve směru normálového vektoru, kde jednotkou je délka tohoto normálového vektoru. Tomto vyjádření se říká obecný tvar roviny v prostoru, nám ale pro účely 3D grafiky bude stačit určení roviny bodem a vektorem.
Závěrem
Jsem si vědom toho, že tento teoretický díl plný potřebných znalostí, měl být na začátku seriálu, ale je to proti mé zásadě "nejdřív nadchnout a pak až rozumět". Pro začátečníky je důležité, aby hned ze začátku něco bylo vidět, což se u 3D tutoriálů dělá poměrně těžko bez znalostí práce s vektory. Pokud vám tedy v minulých dílech nebylo něco jasné, po přečtení tohoto dílu by už být mělo. Příště si ukážeme praktické použití toho, co jsme se dnes teoreticky naučili.
Pokud jste vše, co jsem zde složitě popisoval, už znali dříve, je to jen dobře. Doufám ale, že tento díl pomohl těm, kteří potřebné znalosti nemají nebo si je potřebují oprášit.