dotNETportal.cz

V minulém díle jsme se naučili pracovat se světlem a s texturami, dnes se naučíme zpracovávat vstup uživatele z klávesnice nebo z myši. Naprogramujeme jednoduchou hru, ve které budeme naším známým jednorožcem z druhého dílu. Otevřete si tedy projekt z minula a než začneme, provedeme pár úprav.

Změna textury trávy

Naše tráva na terénu vypadá tak trochu uměle a není z ní zřetelně vidět tvar terénu, takže ji můžeme zkusit vyměnit za tuto texturu. Stáhněte si ji (pravým tlačítkem na ni klikněte a zvolte Uložit obrázek jako...). Teturu uložte do složky Content ve složce projektu a nahraďte jí obrázek grass.jpg.

Úprava opakování textur

Minule jsme do kódu ve třídě Landscape napsali "natvrdo", že textura, kterou terénu přiřadíme, se má opakovat 8x na délku a 8x na šířku celého terénu. Bude lepší, když z této napevno zadané hodnoty uděláme vlastnost třídy Landscape a budeme ji moci nastavovat zvenčí. Naše třída Landscape pak bude univerzálnější. Otevřete si tedy soubor s kódem třídy Landscape a najděte proceduru PrepareVertexBuffer. Řádek začínající .TextureCoordinate opravte takto:

                     .TextureCoordinate = New Vector2(x * _textureScale / width, y * _textureScale / height)

Visual Studio vám samozřejmě nahlásí chybu, protože používáme proměnnou _textureScale, kterou nemáme nadeklarovanou. Odrolujte si tedy kód nahoru a k ostatním deklaracím uvnitř třídy (ne v proceduře!) přidejte tuto vlastnost:

     Private _textureScale As Single = 16F

     Public Property TextureScale() As Single

         Get

             Return _textureScale

         End Get

         Set(ByVal value As Single)

             _textureScale = value

         End Set

     End Property

Nastavení pozice kamery dynamicky

Také pozici kamery jsme do třídy Game napsali "natvrdo", ale nyní s ní budeme potřebovat manipulovat. Najděte tedy ve třídě Game tyto tři řádky:

     Private world As Matrix = Matrix.Identity

     Private view As Matrix = Matrix.CreateLookAt(New Vector3(32, 12, 16), New Vector3(32, 8, 32), Vector3.Up)

     Private proj As Matrix = Matrix.CreatePerspectiveFieldOfView(MathHelper.PiOver4, 4 / 3, 1, 1000)

Smažte je a místo nich vložte tyto deklarace:

     Private posX As Single = 26, posZ As Single = 18, angle As Single = 0

 

     Private world As Matrix = Matrix.Identity

     Private view As Matrix

     Private proj As Matrix = Matrix.CreatePerspectiveFieldOfView(MathHelper.PiOver4, 4 / 3, 1, 1000)

Přidal jsem dvě proměnné posX a posZ, které reprezentují pozici jednorožce, a proměnnou angle, která drží úhel, ve kterém je jednorožec natočen, matici view podle těchto hodnot vždy spočítáme v metodě Update, ale to až později.

Přidání jednorožce

Do projektu si přidejte znovu našeho jednorožce z druhého dílu, ve třídě Game do deklarací přidejte první řádek a do metody LoadContent řádek druhý. Není na tom nic, co bychom neznali.

     Private unicorn As Model

     unicorn = Content.Load(Of Model)("Content\unicorn")

Pokud jste ze svého projektu v některém z minulých dílů neodstranili proceduru RenderModel ve třídě Game, kterou jsme napsali ve 2. dílu, odstraňte ji a nahraďte ji touto verzí, které jsem přidal možnost provádět změnu měřítka. Model jednorožce je totiž v jiném měřítku než terém, je třeba jej 3x zvětšit.

     Public Sub RenderModel(ByVal m As Model, ByVal position As Vector3, ByVal rotation As Double, ByVal scale As Single)

         ' Vykreslit celý model

         Dim transforms(m.Bones.Count - 1) As Matrix

         m.CopyAbsoluteBoneTransformsTo(transforms)

 

         For Each mesh As ModelMesh In m.Meshes      ' projít všechny části modelu

 

             For Each eff As BasicEffect In mesh.Effects     ' všem efektům nastavit pozice

                 ' nastavit všechny 3 matice

                 eff.World = Matrix.CreateScale(scale) * Matrix.CreateRotationY(rotation) * transforms(mesh.ParentBone.Index) * Matrix.CreateTranslation(position)

                 eff.View = view

                 eff.Projection = proj

 

                 eff.EnableDefaultLighting()     ' vypnout standardní osvětlení

             Next

 

             mesh.Draw()         ' vykreslit část modelu

 

         Next

     End Sub

Zjištění výšky terénu v konkrétním bodě

Abychom mohli spolehlivě pozicovat jednorožce po terénu, určitě budeme potřebovat funkci, které předáme souřadnice X a Z nějakého místa a ona nám vrátí přesnou výšku terénu v tomto bodě. Pokud by mohly být souřadnice X i Z jen celočíselné, bylo by to poměrně triviální, ale náš jednorožec vždycky nemusí stát na místě s celočíselnými souřadnicemi, tedy tam, kde výšku známe rovnou. Potřebujeme zkrátka ze souřadnic zjistit, na kterém trojúhelníku se hledané souřadnice nacházejí, a podle vzdálenosti od vrcholů v tomto trojúhelníku dopočítáme výšku. Přesný postup doufám vysvětluje dostatečně tento obrázek:

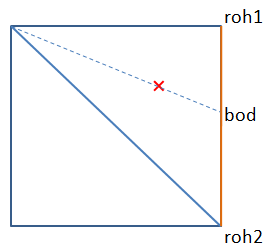
Červený čtvereček určuje bod, ve kterém výšku terénu hledáme. My známe výšku pouze ve všech rozích čtverce. Jednoduchou podmínkou tedy rozhodneme, jestli je bod v pravém či levém trojúhelníku (stačí porovnat souřadnice bodu v rámci čtverce - pokud má červený bod X souřadnici větší než Z, pak je v pravém čtverci, pokud má větší Z, je ve čtverci levém; jen pro doplnění, na světle modré úhlopříčce mají body souřadnice X a Z stejné).

Jakmile tedy víme, ve kterém trojúhelníku bod je, proložíme z jednoho rohu tímto bodem přímku a v místě, kde protne nějakou stěnu čtverce, máme vyhráno. V našem případě máme vyznačenou oranžovou stranu čtverce - na ní se totiž výška mění plynule (lineárně) z jednoho rohu do druhého. Výšku v bodě, kde se protíná s proloženou čárkovanou přímkou, spočítáme pomocí vzorce:

bod.Y = roh1.Y + (roh2.Y - roh1.Y) * (bod.Z - roh1.Z)

Jak to funguje? Představte si, že už víme, kde je bod (známe jeho souřadnici Z), a máte jít z bodu roh1 do bodu roh2. Vaše nadmořská výška na začátku byla stejná, jako v bodě roh1, a jakmile dorazíte do bodu roh2, přičetl se k této výšce rozdíl výšek obou bodů (tedy roh2.Y - roh1.Y). Bod bod je někde řekněme v polovině cesty a výška roste rovnoměrně, proto v bodě bod se k vaší původní nadmořské výšce přičte jen polovina rozdílu výšek na začátku a na konci. My využijeme toho, že víme, že body jsou v naší mřížce rozmístěné ve vzdálenostech 1, takže vzdálenost bodů bod a roh1 bude odpovídat přesně části původní cesty. Když tedy chceme spočítat výšku v bodě bod, k výšce v bodě roh1 přičteme rozdíl výšek bod2.Y - bod1.Y, který vynásobíme příslušnou vzdáleností bod.Z a roh1.Z (jdeme totiž po svislé souřadnici Z), která se pohybuje od 0 do 1 podle toho, kde náš bod je.

Nyní tedy známe výšku v bodě bod. A celý postup můžeme zopakovat ještě jednou, tentokrát s čárkovanou úsečkou. Známe výšky v jejích krajních bodech, jediné, co ještě nevíme, je kde náš hledaný bod na úsečce leží (ve které části). Ale tady nám pomůže Pythagorova věta, známe délku tmavě modré horní strany (to je 1), známe vzdálenost z bodu do rohu1, takže můžeme podle známého vzorce c² = a² + b² dopočítat c, což bude délka čárkované úsečky. No a z rozdílu souřadnic X a Z horního levého rohu a hledaného bodu můžeme opět spočítat vzdálenost těchto bodů (opět použití Pythagorovy věty, proložte si hledaným bodem svislou čáru a uvidíte pravoúhlý trojúhelník, kde jeho dvě kratší strany - odvěsny - mají délky přesně rozdíly souřadnic X a Z horního levého rohu a hledaného bodu).

Pokud jste se ještě neztratili, napadlo vás, že používáme bod bod, ale neznáme jeho Z souřadnici. Tu získáme úplně stejným postupem, akorát rozdíl vynásobíme číslem "o trochu vyšším než jedna". Je to jako kdybyste bod2 přešli a šli ještě dál, pořád budete stoupat a rozdíl se přičte tolikrát, kolikrát více jste urazili než jste urazit měli. A to je přesně ono.

Celému tomuto divadlu, které jsme nyní třikrát použili, se říká lineární interpolace. Zkrátka pro zjištění nějaké mezihodnoty, která plynule přechází z jednoho bodu do druhého, stačí přičíst k hodnotě v prvním bodě rozdíl krajních hodnot, který vynásobíme číslem od 0 do 1, které charakterizuje, na kterém místě v cestě hodnotu zjišťujeme. Čím je toto číslo nižší, tím blíže je u prvního bodu, čím víc se blíží jedničce, tím víc se blíží bodu druhému. Je to vlastně poměr vzdálenosti hledaného bodu a prvního bodu ku celkové délce z jednoho bodu do druhého. Protože tuto operaci budeme provádět vícekrát, vyplatí se napsat si metodu Interpolate, které předáme hodnoty v krajních bodech a koeficient (poměr vzdáleností), a ona nám již výsledek spočítá.

Nebudu to již dále popisovat, zde je kód, který souřadnice spočítá, přidejte jej do třídy Landscape.

     Private Function Interpolate(ByVal val1 As Single, ByVal val2 As Single, ByVal koef As Single) As Single

         'provede lineární interpolaci a vrátí výsledek

         '- val1 a val2 jsou hodnoty v krejních bodech

         '- koef je číslo od 0 do 1 reprezentující vzdálenost od prvního bodu

         Return val1 + (val2 - val1) * koef

     End Function

 

     Public Function GetHeight(ByVal x As Single, ByVal z As Single) As Single

         'pokud jsme náhodou mimo terén, vrátit nulovou výšku

         If x < 0.0F Or z < 0.0F Or x >= width - 1 Or z >= height - 1 Then Return 0.0F

 

         'ošetřit body ve skoro celočíselných vrcholech

         If Math.Abs(x - Math.Round(x)) < 0.001F And Math.Abs(z - Math.Round(z)) < 0.001F Then Return heights(Math.Round(x), Math.Round(z))

 

         'zjistit souřadnice horního levého rohu čtverce

         Dim lX As Integer = Math.Floor(x), lZ As Integer = Math.Floor(z)

 

         'určit, ve kterém trojúhelníku jsme

         Dim rX As Single = x - lX, rZ As Single = z - lZ

         If rX > rZ Then          'pravý trojúhelník

             Dim bodZ As Single = Interpolate(lZ, z, 1.0F / rX)   'spočítat bod.Z

             Dim bodY As Single = Interpolate(heights(lX + 1, lZ), heights(lX + 1, lZ + 1), bodZ - lZ)   'spočítat bod.Y

             Dim koef As Single = Math.Sqrt(rX * rX + rZ * rZ) / Math.Sqrt(1 * 1 + (bodZ - lZ) * (bodZ - lZ))   'spočítat poměr vzdáleností

             Return Interpolate(heights(lX, lZ), bodY, koef)

 

         Else                             'levý trojúhelník

             Dim bodX As Single = Interpolate(lX, x, 1.0F / rZ)   'spočítat bod.Z

             Dim bodY As Single = Interpolate(heights(lX, lZ + 1), heights(lX + 1, lZ + 1), bodX - lX)   'spočítat bod.Y

             Dim koef As Single = Math.Sqrt(rX * rX + rZ * rZ) / Math.Sqrt((bodX - lX) * (bodX - lX) + 1 * 1)   'spočítat poměr vzdáleností

             Return Interpolate(heights(lX, lZ), bodY, koef)

 

         End If

     End Function

Pro pravý trojúhelník počítáme přesně podle postupu uvedeného nahoře, nejprve zjistíme bod.Z, pak spočítáme výšku v bodě Z a nakonec z poměru vzdáleností na čárkované čáře spočítáme finální výšku hledaného bodu. Pro levé trojúhelníky je to to samé, akorát počítáme bod.X. Jinak v proměnných lX a lZ jsou souřadnice levého horního rohu vrcholu a proměnné rX a rZ udávají rozdíly souřadnic hledaného bodu a levého horního vrcholu.

Nasazení jednorožce do terénu

Jednorožce máme již načteného, takže jej můžeme vykreslit. Tento řádek přidejte za vykreslování terénu do procedury Draw uvnitř třídy Game:

 RenderModel(unicorn, New Vector3(posX, land.GetHeight(posX, posZ), posZ), angle - MathHelper.PiOver2, 3.0F)

Pozici jednorožce zjistíme z proměnných posX, posZ a jeho výšku z funkce, kterou jsme napsali před chvílí, tedy land.GetHeight(posX, posZ). Jednorožce otočíme o angle - π/2 stupňů, protože model je otočený o 90 stupňů, což je právě π/2 radiánů.

Ještě jež to bude fungovat správně, musíme nastavit kameru podle proměnných posX a posZ, jak jsem slíbil na začátku. Tento kód přidejte do procedury Update ve třídě Game:

         'kamera se bude dívat na místo, kde je jednorožec, ale na místo 3 jednotky nad zemí

         Dim lookAt As Vector3 = New Vector3(posX, land.GetHeight(posX, posZ) + 2, posZ)

         'spočítat pozici kamery v závislosti na natočení jednorožce

         Dim camPos As Vector3 = New Vector3(1.5 * Math.Sin(angle), 0.2, -1.5 * Math.Cos(angle))

         'vytvořit matici výhledu

         view = Matrix.CreateLookAt(lookAt + camPos, lookAt, Vector3.Up)

Do proměné lookAt si připravíme vektor se souřadnicemi posX a posZ, tedy se souřadnicemi jednorožce. Jako souřadnici Y mu ale předáme výšku terénu v tomto bodě + 3 jednotky, abychom se nedívali jednorožci pod nohy, ale viděli mu přes hlavu, musíme prostě být kus nad zamí. Na tuto pozici bude totiž kamera mířit.

Proměnnou camPos, která udává pozici kamery vzhledem k pozici jednorožce, počítáme rotací vektoru 0, 0.2, -1.5 kolem osy Y podle aktuálního úhlu. Takže souřadnici Z tohoto vektoru násobíme hodnotou Math.Cos(angle), když je úhel 0, pak je hodnota funkce kosinus 1, takže se souřadnice Z násobí jedničkou, kdežto souřadnice X se násobí hodnotou sinus 0, což je 0. Pokud měníme proměnnou angle, budou se hodnoty plynule přelévat tak, aby se vektor otáčel správně. Z těchto dvou vektorů pak vytvoříme matici kamery.

Pohyb jednorožce

Pohyb jednorožce bude poměrně jednoduchý, ale je třeba dát si pozor na pár věcí. Navíc se naučíme, jak pracovat s klávesnicí a myší z XNA. Nemáme totiž žádné události, jako normálně, musíme si stavy zjišťovat sami. Stav klávesnice zjistíte zavoláním Keyboard.GetState(). Je dobré si v každém snímku zjistit stav jen jednou a neptat se na něj pořád. Ve VB.NET jsou na to ideální bloky With. Následující 2 bloky kódu vložte postupně do procedury Update nad vypočítávání pozice kamery.

         Dim hopping As Double = 0

         'reagovat na ovládání klávesnicí

         With Keyboard.GetState()

             If .IsKeyDown(Input.Keys.Up) Then   'jedeme dopředu

                 posX += -Math.Sin(angle) * gameTime.ElapsedGameTime.Milliseconds * 0.01F        'posunout jednorožce

                 posZ += Math.Cos(angle) * gameTime.ElapsedGameTime.Milliseconds * 0.01F

                 hopping = 0.09 * Math.Sin(gameTime.TotalGameTime.TotalMilliseconds * 0.006F)    'efekt hopsání

             ElseIf .IsKeyDown(Input.Keys.Down) Then  'couváme

                 posX -= -Math.Sin(angle) * gameTime.ElapsedGameTime.Milliseconds * 0.005F        'posunout jednorožce

                 posZ -= Math.Cos(angle) * gameTime.ElapsedGameTime.Milliseconds * 0.005F

             End If

         End With

V tomto kusu kódu ovládáme jízdu jednorožce. Bude umět jezdit dopředu a při tom bude ještě hopsat, a také bude umět couvat, ale to bude dělat pomaleji a u toho už hopsat nebude. Založíme si tedy proměnnou hopping, kde bude vzdálenost, o kterou se bude vychylovat svisle kamera, aby to dojem hopsání navodilo.

Dále si zjistíme stav klávesnice a metodou IsKeyDown se ptáme na konkrétní klávesu, jestli je stisknutá. Pokud je stisknutá klávesa nahoru, do proměnných posX přičítáme vhodný násobe funkcí Sin a Cos pro aktuální natočení jednorožce vynásobený hodnotou gameTime.ElapsedGameTime.Milliseconds, což je počet milisekund, kolik zabralo vykreslování posledního snímku. Na každém počítači totiž může být počet snímků různý a pak by také jednorožec jezdil všude různě rychle. Když rychlost posunu 0.01 vynásobíme počtem milisekund, dostaneme hodnotu, o kolik milisekund se má jednorožec posunout. Pokud se tedy stihnul za 30 milisekund 1 snímek, jednorožec se posune o 0.3, pokud se stihnuly 2 snímky, jednorožec se posune 2x, ale pokaždé o 0.15, takže ve výsledku je to stejné.

Nakonec do proměnné hopping přidáme hodnotu vynásobenou opět nějakou hodnotou Sin, kde gameTime.TotalGameTime.TotalMilliseconds je celkový počet milisekund, který uplynul od začátku hry. Jako výsledek bude hodnota proměnné hopping kolísat v sinusovém rytmu, tedy bude se plynule měnit od -0.09 do 0.09, dokud jednorožec pojede. Možná si říkáte, že dost často něco násobíme nějakou konstantou, ale sami byste na to nepřišli, že ta konstanta bude zrovna takto. Když navrhujete kód, musíte metodou pokus-omyl vymyslet, jaké ty konstanty budou, aby to hezky vypadalo.

Nyní se vrhneme na otáčení výhledu jednorožce. To nám zajistí tento kód:

         'zatáčet pomocí myši

         With Mouse.GetState()

             'otáčet pohled

             angle += (.X - Me.Window.ClientBounds.Width / 2) * 0.006F

             'vrátit myš doprostřed okna

             Mouse.SetPosition(Me.Window.ClientBounds.Width / 2, Me.Window.ClientBounds.Height / 2)

         End With

Z Mouse.GetState() si zjistíme stav myši a používáme vlastnosti .X a .Y se souřadnicemi myši vzhledem k levému rohu okna. Podle vzdálenosti kurzoru od prostředku okna určíme hodnotu, která se má přičíst do proměnné angle. Po odečtení nastavíme kurzor doprostřed okna, aby nám neujel na konec obrazovky, pak bychom již nemohli otáčet na obě strany.

To je skoro vše, ještě poslední věc, upravte přepočítávání pozice kamery takto, aby se bralo v úvahu hopsání jednorožce, které v předchozí verzi nebylo:

         'kamera se bude dívat na místo, kde je jednorožec, ale na místo 3 jednotky nad zemí

         Dim lookAt As Vector3 = New Vector3(posX, land.GetHeight(posX, posZ) + 2, posZ)

         'spočítat pozici kamery v závislosti na natočení jednorožce

         Dim camPos As Vector3 = New Vector3(1.5 * Math.Sin(angle), 0.1 + hopping, -1.5 * Math.Cos(angle))

         'vytvořit matici výhledu

         view = Matrix.CreateLookAt(lookAt + camPos, lookAt, Vector3.Up)

A to už byla poslední úprava, nyní se s naším jednorožcem budeme moci po terénu projet. Jen podotýkám, že kurzor myši se bude pořád držet uprostřed okna, takže jej budete muset zavřít přes Alt-F4. Nebo si do procedury Update můžete přidat ukončení hry při stisku klávesy Escape, to už je na vás.

Doufám, že se příliš neztrácíte v matematice, začíná toho být moc. Příští díl asi bude obsahovat teoretickou část o goniometrických funkcích sinus a kosinus, abych měl jistotu, že všichni rozumí tomu, co děláme. Pokud máte nějaké další nápady nebo potřebujete něco lépe vysvětlit, napište do diskuse.

Pokud jste se někde ztratili nebo jste se někde přehlédli, můžete si stáhnout zdrojové kódy.