Poslední dobou jsem ve volném čase mezi školními povinnostmi programoval hru HexaLines pro zařízení s Windows Mobile. Před několika dny jsem ji dokončil, už si ji můžete koupit v obchodu PocketGear. K dispozici jsem dal na odzkoušení i omezenou demoverzi zdarma. Pro více informací se můžete podívat na http://hexalines.com, najdete tam i aktuální rozcestník s odkazy na recenze, články a videa.
Jeden článek o vývoji jsem už sem kdysi psal, přesto bych se rád podělil o další poznatky. Článků možná vydám několik, ale raději nic slibovat nebudu, kvůli času. V tomhle se zaměřím na to, jak jsem ve hře řešil umělou inteligenci. Mohl by vám dát určitý pohled pod pokličku hry i například poskytnout nějaké nápady na strategie, jak hrát hru lépe.
Pravidla a přesné chování hry
Připomenul bych zde v krátkosti pravidla hry. Na první pohled se můžou zdát složitá, ale dají se vcelku rychle pochopit. Ve hře si je můžete osvojit v interaktivním tutoriálu.
Tato 2D strategická puzzle hra je pro tři hráče, můžete ji hrát proti svým přátelům na jednom PDA, nebo proti umělým inteligencím. Cílem každého hráče je zaplnit co nejvíce cestiček svojí barvou, která vytéká ze zdroje z prostřední buňky. Hraje se s šestiúhelníkovými buňkami, ve kterých je vždy vygenerovaný nějaký tvar vnitřních cestiček (existuje celkem 45 různých).
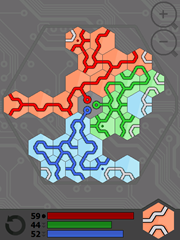
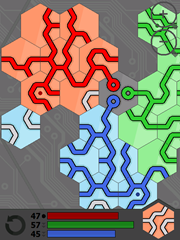
Hráči se střídají v tazích. V každém tahu můžete buď přidat na plán buňku, kterou vidíte dole, nebo s nějakou už umístěnou otočit. Přidat můžete jen tak, abyste přiložili buňku k ostatním, nemůžete ji položit do volného prostoru. Pokud buňku vložíte tak, že prodloužíte délku cesty své barvy, buňka se zabarví vaší barvou, jinak zůstane světle šedá. Otáčet můžete jen buňkami své barvy, světle šedými buňkami může otáčet úplně každý. Proto je dobrá taktika vždy přidávat buňku tak, abyste rovnou navázali na cestu své barvy a protivník vám už s ní nemohl otáčet (využívat se dá ale i chování světle šedých buněk).
Přidáním nebo otočením buňky se může stát, že vlijete barvu do cesty jiné barvy. V tom případě bude navazující buňka zničena. Pokud vlijete barvu přímo do zdroje protivníka, zabijete ho. Přepočítávání barev probíhá v opačném pořadí, než jdou hráči, tj. nejdřív se přepočítá červená, pak modrá a nakonec zelená. Při jedné akci se tedy může odbouchnout víc buněk kaskádovitě a také tedy můžete využívat ve své taktice i tok barvy protivníka. Toto odbouchávání se chová intuitivně tak, jak by člověk očekával, tj. pokud vidíte v navazující buňce protivníkovu barvu a vy do ní změnou situace navážete svoji, bude určitě odbouchnuta (nezávisle na tom, že po pootočení by se tam ta barva třeba ani nemohla dostat). Nejsou tedy proti pravidlům ani takové situace, kdy si např. sami odbouchnete buňku, skrz kterou tam vaše barva přitékala.
První buňka pro každého hráče je vždy vygenerována tak, aby nemohl získat velkou výhodu. Vždy půjde přiložit na jeho zdroj a bude mít alespoň dva výjezdy do volného prostoru. Další buňky už jsou generovány náhodně. Pokud se vrátí tah zpátky, vygenerují se stejné buňky, jako byly předtím. Hra končí, pokud je celý šestiúhelníkový plán zaplněn buňkami, nebo pokud už zbyl jediný hráč. Vyhrává ten s nejdelší cestou, hra může také skončit remízou.
Přepočítávání herního plánu
Problém herní AI by se dal rozdělit do dvou hlavních částí. Jak řešit samotné přepočítávání herního plánu, rozlívání barev a odbouchávání buněk, jak má být plán reprezentován a co bychom si při přepočítávání mohli pamatovat. Zadruhé, jak sestavit rozhodovací algoritmus pro umělou inteligenci, jejíž objekt sedí nad herním plánem, dívá se na něj stejně jako každý jiný hráč a snaží se ze všech dostupných informací vymyslet co nejlepší tah (případně, jak a jestli dát AI nějakou výhodu nad hráčem, aby nad ním mohla trochu podvádět).
Přepočítávání plánu je víceméně přímé, stačí vždy vynulovat konkrétní barvu z plánu a postupně z každého zdroje spustit rozlévání tekutiny po buňkách. To se dá udělat průchodem do šířky nebo do hloubky (backtrackingem). Je si potřeba dát pozor na to, že jedna buňka nemusí odpovídat jednomu uzlu ve stromu, ale více; v jedné buňce mohou být až tři různé segmenty naplněné různými barvami. Při zaplňování segmentů je potřeba také detekovat, jestli se nevlila jedna barva do druhé a případně tuto buňku vymazat. Protože odbouchávání buněk může způsobit, že by tam zůstaly segmenty zaplněné barvou, která už do nich nemohla přitéct, musí se volat dokola přepočítávání do té doby, kdy už na plánu nebude žádná změna.
Já jsem použil průchod do hloubky pomocí rekurzivní metody (backtracking). Jde ze zdrojového segmentu konkrétní barvy. Pokud narazí na volnou cestu, zanoří se do dalšího segmentu a znovu projde, do kterých dalších segmentů se z něho dá dostat. Pokud se narazí na cizí barvu, odbouchne buňku, podobně se ošetří vlití barvy do zdroje protivníka. Pokud už to dál nejde, vrací se v rekurzi zpět. Je si to potřeba ohlídat, aby to fungovalo správně. Tvar zaplněných cestiček totiž obecně nemusí být stromeček, mohou tam vznikat cykly. Je tedy nutné si nějak značkovat, skrz které segmenty jsme do toho konkrétního přišli. Před zanořením do rekurze tedy segmentu nastavujeme značku, že na něj v rekurzi nemáme vstupovat, při vynořování ji zase odstraňujeme.

Pro další využití se při tomto vynořování z rekurze hodí ukládat do segmentů i další data. Přinejmenším délku podstromu pro umělou inteligenci určitě využijeme. Celkovou délku barvy potom dostaneme jako hodnotu celého stromu ve zdrojovém segmentu. Je si ale potřeba dát pozor na chování cyklů. Do konkrétního segmentu se mohlo vstoupit z více stran, hledání do hloubky si ale vybralo jen jednu konkrétní (veškeré segmenty dané barvy vlastně prošlo jen jako strom, hodnoty podstromů budou odpovídat právě tomuto konkrétnímu stromu). Hledání do šířky by nám možná dalo lepší tvar stromu, backtracking mi ale přišel příjemnější na napsání.
Aby s tím AI neměla takový problém, ještě se do každého segmentu zapamatovává směr barvy, ze kterého tam přitekla. Konkrétní hrany nastavíme jako přítokové (odtokové) právě tehdy, když právě těmito hranami se při hledání do hloubky přešlo z jednoho segmentu do druhého. Koncovým hranám, případně hranám, skrz které jsme kvůli značce nešli (tvořily by cyklus), nenastavujeme nic. Před samotným přepočítáváním je potřeba mít všechny směry i hodnoty podstromů vynulované, aby tam nemohl nastat problém.
I když to s přepočítáváním plánu nesouvisí, je pochopitelně nutné udržovat herní plán v každé chvíli v konzistentním stavu, aby byly nastaveny správně všechny odkazy mezi segmenty/buňkami, především po operacích vkládání, otáčení a mazání. Aby nenastal problém při vracení tahů zpátky nebo při speciálním chování hry např. na začátku. Přepočítávací metoda také musí například správně ošetřovat stav, když si sama smaže buňku pod sebou (viz. pravidla na začátku) a už se nemůže vrátit z rekurze zpět.
AI - globální přístup
Samotná umělá inteligence by se mohla řešit mnoha způsoby. Je potřeba z možných tahů vybrat ten nejvýhodnější, přičemž se uvažují všechny možnosti, kam se dá buňka vložit a kterými všemi buňkami se může pootočit (kde ještě je 5 možností, o kolik stran se můžou natočit). Posuzovat to jde buď lokálně (ohodnotit si tahy a z nich vybrat ten nejlepší), globálně (předpokládat, co se stane a zanořit se několik tahů do budoucnosti), nebo kombinací obou přístupů.
Globální přístup by vyžadoval drobný podvod na hráče, AI by předem věděla, jaké buňky budou následovat. Potom by si mohla nasimulovat všechny možné tahy např. na čtyři tahy dopředu, s tím, že by si pro sebe simulovala i hru ostatních hráčů. Z poslední hladiny tahů by vybrala ten s největší délkou trasy a provedla by tah tímto směrem. Výhodou by bylo, že by se možná dokázala vyhrabat i ze slepých uliček. Samotná posuzovací metoda by také mohla být poměrně jednoduchá, počítalo by se např. jen se získanou délkou cesty a s počtem volných výjezdů.
Tímto směrem jsem se ale nevydal, z několika důvodů. Počet možných kombinací, zvlášť kvůli možnosti otáčení na různé strany, by mohl být hodně velký. I s nějakou heuristikou a prořezáváním by s tím malá PDAčka mohla mít docela problémy. Napsat a odladit takovouhle rekurzivní proceduru by také nemuselo být úplně jednoduché. Navíc by se stejně nemohlo pracovat s přesnými výsledky, pokud bychom pro každou možnost volali přepočítávání plánu, abychom zahrnuli i možnost smazání buněk (prováděli bychom to např. na nějaké kopii plánu), bylo by to už opravdu pomalé. Věřím, že by se tato strategie mohla chovat zajímavě, nakonec jsem se ale pustil do víceméně lokálně se chovající verze (s pár drobnostmi navíc). Jde víceméně o specifické problémy této hry, že například příchozí buňky mají hodně náhodný charakter a hrací pole se v každém tahu může hodně měnit. Moje výsledná AI nakonec ale funguje dobře, další vylepšování by už asi nepřineslo nic moc navíc.
Můj přístup - ohodnocení tahů
Můj přístup by se dal rozdělit na tyto základní kroky:
- Zjištění si všech možných tahů, které AI může provést
- Ohodnocení tahů pomocí několika parametrů
- Výběr nejlepšího tahu
Přičemž při ohodnocování daného tahu (přidání, otočení) se dívám jen na okolní segmenty/buňky a podle hodnot v nich uložených odhaduji, kolik toho daný tah přinese. Není to metoda úplně přesná (vzhledem k tomu, jak jsme procházeli strom do hloubky a ohodnocovali segmenty) a občas se může splést (např. brát nějaký tah jako moc výhodný), ale je to metoda rychlá. Když se k ní přidá ošetření pár speciálních případů a ochrana proti zacyklení (popíšu později), chová se dobře.
Každý tah je ohodnocen těmito šesti parametry, nezávisle na tom, jestli je to přidávání nebo otáčení:
- Kolik bodů získá (nebo ztratí) tímto tahem. Uvažuje se, jakou délku barvy získá + co ubere smazáním dalších buňek (pokud přelije barvu do segmentu jiné barvy), mínus to, kolik se případně do ostatních segmentů této buňky (a dál) vlije jiná barva. K tomu, jak to bylo naprogramováno, aby se to chovalo správně, se ještě vrátím.
- Jestli přikládá buňku k buňce své barvy, neboli, jestli se nenapojuje na buňku, se kterou by mohl otáčet i někdo jiný. Na stejné úrovni jako tato podmínka je také, jestli otáčí s buňkou své barvy.
- Kolik získá různých výjezdů své barvy do volného prostoru. Počítají se jen získané výjezdy do stran, kam s barvou ještě nemířil. Je to proto, že pokud AI nemůže přidat novou buňku, snaží se ty na plánu otáčet tak, aby měla co největší pravděpodobnost, že bude moci znovu přidat. Neuvažuje zde žádný konkrétní směr (příští buňka může být úplně jiná), ani neuvažuje, kolik by zablokovala cizích výjezdů. To by byla moc defenzivní taktika, vkládalo by se moc šedých buněk a nechovalo by se to dobře. Počet získaných výjezdů pro daný tah může ale být pochopitelně i záporný.
- Kolika se zbaví výjezdů své barvy do stěn buněk jiných barev. Snaží se, aby směrem k protivníkům vystavovala co nejméně svých výjezdů. Kryje se tím tak proti tomu, aby jí tuto buňku nemohl protivník pootočením vyhodit.
- Jestli nepřidává, ale otáčí. Toto je ošetření proti vkládání velkého množství šedých buněk na plán. Raději otočí s nějakou buňkou, než aby přidávala náhodně.
- Kolik napojí prázdných výjezdů na další prázdné. Pokud už přidává šedou buňku (nenapojuje se na svoji barvu), snaží se ji alespoň přidat tak, aby cestičky tvořily co největší spojitý úsek, ne jen náhodné kousíčky.
Při výběru tahu jdeme postupně od prvního k šestému parametru, přisuzujeme jim snižující se prioritu. Pokud existuje jediný nejlepší tah, vybereme ten; pokud jich existuje víc srovnatelných, vybereme z nich jeden náhodně. Interně je to zařízeno tak, že je List možných tahů, které mají naimlementovaný interface IComparable s metodou CompareTo(). Na tento seznam tahů se potom zavolá metoda Sort().
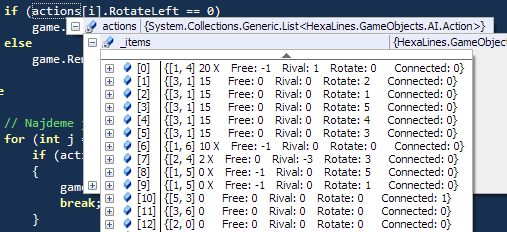
Výběr tahu
Před samotným provedením tahu ještě ošetříme několik drobností. Pokud už zbývá jediné volné políčko a AI by vložením buňky vyhrála (měla nejvíce bodů), určitě tento tah provede. Dále pokud může pootočit buňku tak, že zabije protivníka vlitím barvy do jeho zdroje, také to udělá. Vzhledem k seřazení možných tahů podle priorit vybere tu nejlepší možnost, jak ho zabít. Protože by si ale v tomto případě mohla nějak rozhrabat to, co už tam dlouho budovala, zapamatuje si tento tah a v příštím tahu se pootočí zpátky.
Tuto podmínku o vlití barvy do zdroje jsem nakonec nechal jen pro otáčení, pro případ přidávání by se dalo udělat něco podobného s ošetřením „pokud si sama neubere moc bodů“. Určitě by se ještě hodil například ošetřit případ, kdy už ona hraje jen proti jednomu hráči a mohla by přidáním buňky rovnou vyhrát, nechtěl jsem to ale moc komplikovat dodatečnými podmínkami.
Dalším extra případem je stav, kdy má před zdrojem prázdné políčko a mohla by tam rovnou přidáním navázat buňku. V této chvíli nemá cenu zachraňovat nic na plánu (např. vyhazovat protivníkovou barvou buňku druhého), ale raději se krýt, i kdyby si tam měla položit buňku s nevýhodným tvarem. V jiných případech se už ale provede jeden z těch nejlepších tahů.
Ochrana proti zacyklení
Je potřeba zařídit, aby se AI při hraní nemohly dostat do slepé uličky. Speciálně v případech, kdy by hrály jen proti sobě, by si mohli s nějakou buňkou donekonečna otáčet a hra by nikdy nemusela skončit. Pro každý tah před jeho provedením se tedy zkontroluje, zda už nedochází k zacyklení. Cyklus se detekuje tak, že se prochází posledních 12 tahů a kontroluje, zda se neopakují poslední 2 tahy, 3 tahy atd. až 6 tahů. Pokud se zjistí, že se dvakrát za sebou provedla stejná řada akcí, vybere se takový nejlepší tah, ve kterém se přidává na plán (neotáčí) a ten se provede. Takový tah musí vždy existovat, jinak by musel být konec hry. Obdobně se za cyklus považuje také to, pokud AI posledních 6 tahů jen otáčela a nic na plán nepřidávala.
Takové řešení je pro tento typ hry dostačující, za 6 tahů se většinou na plánu změní tolik věcí, že delší cykly bychom nejspíš stejně ani okem neodhalili. Nejčastěji takový problém nastává, pokud se dvě AI přetahují o otáčení šedé buňky, v naprostých případech jsou to stejně cykly maximálně délky 2-3.
Řešení umělé inteligence
Přímo z herního objektu se dají vyčíst nějaké informace, jako například pole odkazů na políčka, kam se může vkládat, nebo celkový seznam všech buněk na plánu. V samotných segmentech/buňkách jsou potom uložené předpočítané délky podstromů a směry toku barvy (z hledání do hloubky). Každá buňka si také drží předpočítané odkazy na okolní segmenty/buňky a odkazy, ze které strany kam se dá dostat. Všechno je to proto, aby následné posuzování tahů bylo pro AI co nejrychlejší. Sama pro sebe si AI sestaví ještě seznam odkazů na buňky se kterými může aktuálně otáčet a kolikrát a na jaké směry už míří výjezdy její barvy do volného prostoru.
Pak už se můžou začít konečně ohodnocovat tahy. Nejdřív ty, kde se přidává nějaká buňka a potom i všechny možnosti pootočení. I když se jim posuzují vlastně stejné parametry, jsou tyto akce odděleny do dvou metod, pro větší přehlednost a pohodlnost při ladění.
Samotné programování AI byla docela piplačka, muselo se jít pomalu a postupně, ověřovat malé části kódu, aby se do toho nezamotalo. Měl jsem mnoho testovacích nákresů na papír, hodně času jsem strávil laděním. V případě objevené chyby bylo potřeba odlišit, zda to byla chyba v kódu, nebo v tu chvíli správné chování, ale dané špatně rozmyšleným návrhem. Některé situace nastávaly opravdu jen zřídka, hodně naštěstí pomohlo to, že se mohl pseudonáhodnému generátoru znovu předložit stejný seed a situaci jsem si mohl znovu nasimulovat. Super bylo, že jsem si PDAčko mohl brát do postele a na možné chyby přicházet vleže :) Vymýšlení umělé inteligence a přemýšlení nad jejími okrajovými případy mě rozhodně bavilo...
Ohodnocení přidávání buňky - konkrétně
Postup ohodnocení přidávání buňky je v podstatě přesně stejný, jako bylo už napsáno. Procházejí se její sousedi (strany/segmenty buněk, ke kterým ji přikládáme), pokud se narazí na přítokovou cestu její barvy, přičte se délka segmentu, kam by se barva do ní vlila. V pomocném objektu se pamatuje zaplnění buňky, abychom segment nenaplňovali dvakrát stejnou barvou z různých stran. Posoudí se, zda by mohla tato barva protéct skrz buňku dál do segmentů dalších buněk. Pokud by vtekla do prázdné cesty, přičte se délka tohoto segmentu (nemůže se vědět, jak dlouhý zde navazuje úsek, zkoumají se jen okolní buňky), pokud by natekla do cesty jiné barvy, přičte se délka tohoto podstromu (předpokládá se, že se usekla celá větev).
V dalším kroku se posuzuje, zda by se do nějakých segmentů mohla vlít také barva protivníků. Uvažujeme jen ty segmenty, které jsou ještě stále prázdné (nenatekla tam její barva). Pokud se tak stane, odečteme délku tohoto segmentu, přelijeme barvu, případně ještě posoudíme, pokud se náhodou nemohla dostat dál. Pokud přetekla do prázdné cesty, odečteme délku tohoto segmentu. Pokud přetekla do jiné barvy, naopak přičteme celou hodnotu podstromu (předpokládáme, že protivníkova barva zničila druhého protivníka), je si tady potřeba dát pozor na pořadí toku barev.
Potom se můžou ověřit další parametry. V jednom cyklu se napočítá, kolik výjezdů její barvy do volného prostoru se nyní zakrylo okolním buňkám. Zajímá nás jen, o kolik různých směrů přijde, snižujeme předpočítané hodnoty počtu výjezdů pro každou stranu. Když některý dosáhne nuly, odečteme jedničku od naší hodnoty volných výjezdů (parametr č. 3). Ve stejném cyklu se také napočítá počet vjezdů jeho barvy směřujících do cizí buňky a počet na sebe navázaných prázdných cest. V následném cyklu zjistíme, kolik by získal nových různých výjezdů jeho barvy do volného prostoru a přičteme k parametru č. 3.
Ohodnocení otáčení buňky
Postup ohodnocení otáčení buňky je možná o něco složitější (a o to zajímavější), přesto bych ho vzal už jen v rychlosti. Pracuje se se dvěma stavy buňky - s původním a se stavem po otočení. Nový stav má nastaveny prázdné cesty, nalívají se do něj postupně barvy podobně jako při přidávání buňky. Je udělaná metoda, která pro zadanou barvu vrátí, o jakou délku se prodlouží po otočení buňky. K výsledné délce barvy, která nás zajímá, se přičte hodnota pro naši barvu a postupně odečtou hodnoty pro obě barvy protivníků.
V této metodě přicházejí na řadu přítokové a odtokové směry buněk. Pokud v nějakém segmentu starého umístění byla zvolená barva, určitě měla nějakou přítokovou stranu. Využijeme informace, kterou máme uloženou z prohledání do hloubky, tyto stěny si poznamenáme jako přítokové. Do nového umístění by se ale mohla barva dostat i jinudy, označíme si tedy jako přítokové i ty strany, kde u starého umístění tekla zvolená barva do stěny. Musí se pohlídat platnost invariantu, aby každý segment měl jen jednu přítokovou stranu. Pro každou skutečně vtokovou hranu (ne do stěny) odečteme délku celého jejího podstromu.
Ze všech segmentů se vstupní hranou mohlo existovat několik výstupních směrů, nebo i žádný. Zapamatujeme si tyto odtokové směry a délky jejich podstromů. Doteď se posuzovala situace původního stavu buňky, nyní začneme řešit nové pootočení. Pokud některý ze zapamatovaných přítokových směrů nově navázal do prázdné cesty, přičteme délku segmentu, rozlijeme barvu do nového stavu a podíváme se, jestli by se dal rozlít dál.
Pokud se barva dále rozlije do prázdné cesty, přičteme hodnotu segmentu. Pokud se rozlije do cesty stejné barvy a tento výjezd je zapamatovaný jako odtokový, přičte se zapamatovaná hodnota (v této verzi HexaLines 1.0 je na tomto místě malá chyba v podmínce, kvůli které se občas AI zachová divně, nestává se to ale moc často). Pokud se zvolená barva přelije do jiné barvy, odečte se zase délka podstromu. Pokud se navíc vlije do protivníkova zdroje, poznamená se o tom do akce informace.
V posledních dvou cyklech odečtu, kolik mělo staré umístění různých výjezdů zvolené barvy ven, kolik bylo výjezdů do stěn protivníka a kolik na sebe navázaných prázdných výjezdů; a totéž přičtu pro nové pootočení.
Závěr
Doufám, že tento článek byl pro vás příjemným nahlédnutím do toho, čím jsem se zabýval poslední půlrok. O HexaLines by se toho dalo napsat ještě asi hodně, o architektuře aplikace, o vykreslování hry apod. nebo nějaké ohlédnutí za vývojem. Uvidím, k čemu se ještě dostanu, rád bych se teď zase pustil do dalších činností.