dotNETportal.cz

Shrnutí: Nejdřív si zopakujeme základní pojmy a ujistíme se, k čemu je nám vlastně třídění dobré. Pak si dokážeme, proč to v obecném případě nejde v lepším asymptotickém čase, než O(n * log n). Projdeme si třídění počítáním (Counting sort) a přihrádkové třídění (Bucket sort). Zmíníme Radix sort a od lexikografického třídění k-tic se postupně dostaneme k samotnému třídění řetězců, které si popíšeme podrobněji a dokážeme.

Základní pojmy

Pro řešení úloh pomocí výpočetní techniky potřebujeme mít nástroj, kterým dokážeme porovnat efektivitu a rychlost vykonávání jednotlivých algoritmů. Asymptotická složitost určuje operační náročnost tak, že zjišťuje jakým způsobem se bude chování algoritmu měnit v závislosti na změně počtu vstupních dat (= n). Zapisuje se pomocí „velké O notace“ jako O(funkce n), tj. např. O(log n). Používaný zápis znamená, že náročnost algoritmu je menší než tato f(n) * c1 + c2, kde c1 a c2 jsou vhodně zvolené nenulové konstanty. Zanedbáváme tedy multiplikativní i aditivní konstanty, které stejně většinou závisí na konkrétním počítači, zajímá nás jen chování funkce pro velké hodnoty n, tzn. O(n+100) = O(20n) = O(n). Obvykle uvažujeme časovou a prostorovou asymptotickou složitost. Například O(n²) znamená, že pokud se zvýší délka vstupu 3krát, potřebný čas (paměť) se zvýší 9krát. Takto je to zjednodušeně řečeno, jinak by bylo nutné tyto pojmy nadefinovat přesněji.

Podobně můžeme chování algoritmu odhadovat zespodu, což se zapisuje pomocí velké omegy – Ω(funkce n). Znamená to, že náročnost algoritmu je vždy stejná nebo větší, než nějaký násobek f(n). Ještě se používá velká théta, kterou vyjádříme, že se dá náročnost ohraničit shora i zdola nějakými c1 a c2 násobky f(n) – Θ(funkce n), neboli, že algoritmus bude v nejlepším i nejhorším případě právě takový. Některé složitosti mají i svá jednoduchá pojmenování, např. O(1) – konstantní, O(log n) – logaritmická, O(n) – lineární nebo již zmiňovaná O(n²) – kvadratická.

Tříděním je myšleno seřazení daného souboru dat podle specifikovaného pořadí, nejčastěji podle numerické velikosti čísel, nebo abecedně. I když se v literatuře pro tuto operaci někdy používá výraz řazení, naším tříděním není myšleno pouze rozdělení dat do skupin podle zadaného kritéria, bez určení vzájemného pořadí.

Proč třídit?

K čemu je nám vlastně třídění dobré, proč bychom potřebovali seřadit množinu dat podle nějakého klíče? Nemusí to být jen pro přehlednost, díky tomu také můžeme rychle vyhledávat prvky, konkrétně v čase O(log n), např. pomocí půlení intervalů. Můžeme si to představit na příkladu telefonního seznamu, kdyby byla jména v náhodném pořadí a my chtěli najít nějaké konkrétní, museli bychom projít v nejhorším případě celý seznam, tj. mělo by to časovou složitost O(n). V setříděném seznamu se nám stačí podívat do poloviny, pak čtvrtiny apod. a za nějakých 10-15 testů máme nalezeno.

Obdobně, pokud bychom chtěli zjistit, zda se v dané posloupnosti některé hodnoty opakují, je dokázáno, že to nejde vyřešit rychleji, než tak, že hodnoty nejdřív setřídíme a pak setříděnou posloupnost projdeme.

O(n * log n) v nejlepším případě

Všechny běžné třídící algoritmy jako např. Heapsort, Merge sort nebo Quicksort mají v nejlepším případě časovou složitost O(n * log n). My můžeme dokázat, že v obecném případě ani žádný efektivnější postup neseženeme. Každý třídící algoritmus, ve kterém pouze porovnáváme a prohazujeme prvky (neznáme předem např. rozsah hodnot na vstupu), totiž potřebuje na svůj vstup délky n v nejhorším případě alespoň Ω(n * log n) porovnání.

Důkaz je poměrně jednoduchý. Bez újmy na obecnosti budeme nejdříve předpokládat o algoritmu dvě věci:

• nejprve všechny prvky porovnává, až poté je prohazuje (tato podmínka nám v ničem neuškodí, u každého algoritmu si můžeme průběžně pamatovat, jak se budou prvky prohazovat a promíchat je až na konci)

• vstupem je permutace na množině {1, ..., n} (neboli všechny možné seřazení různých čísel od 1 do n)

Chování tohoto algoritmu popíšeme rozhodovacím stromem. V něm vnitřní vrcholy určují jednotlivá porovnávání prvků, tj. každý odpovídá jednomu stavu algoritmu. Listy (vrcholy, které nemají syny) odpovídají okamžikům, kdy algoritmus přestal porovnávat a prohodil prvky. Výpočet pro daný vstup je potom cesta od kořene do konkrétního listu.

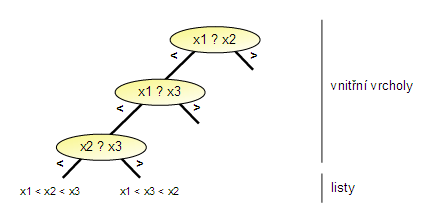
Protože je vstupem permutace n prvků a víme, že počet různých permutací je n! (n faktoriál), existuje tedy právě n! různých vstupů. Dále si všimneme, že abychom je dokázali setřídit všechny, nemůžou existovat dva různé vstupy, pro které by algoritmus skončil ve stejném listu. Listů stromu je tedy alespoň tolik, kolik je různých vstupů, tedy n!.

V našem dalším uvažování vyjdeme z toho, že náš rozhodovací strom je binární, neboli, že každý vrchol má nejvýše dva syny. To platí proto, že jednotlivé prvky na vstupu jsou navzájem různé, vždy je můžeme porovnat a vydat se dále jednou nebo druhou větví. Platí, že binární strom hloubky k má nejvýše 2^k listů.

Je to tak, protože pokud má maximální počet listů, určitě všechny leží na poslední hladině. Kdyby neležely, můžeme pod některý list na vyšší hladině přidat další dva vrcholy a získat tak stejně hluboký strom s více listy. Jelikož na i-té hladině je nejvýše 2ⁱ vrcholů (tj. 1, 2, 4, 8...), všech listů je nejvýše 2^k.

Z toho plyne, že rozhodovací strom musí být hluboký alespoň log n!. Faktoriál můžeme odhadnout zespodu jako n! ≥ n^n/2, důkaz tohoto se dá udělat jako snadné cvičení z diskrétní matematiky. Hloubka stromu je tedy minimálně log n! ≥ log n^n/2 = n/2 * log n = Ω(n * log n), což také zdola odhaduje počet porovnání, který algoritmus provede v nejhorším případě.

Třídění počítáním (counting sort)

Pokud obecně nemůže existovat žádný efektivnější algoritmus, jak je tedy možné třídit v lineárním čase? Postupně si projdeme několik algoritmů využívajících znalosti rozsahu hodnot na vstupu a toho, že je tento rozsah malý. Snažil jsem se přiblížit základní typy, podobných algoritmů je ale hodně, často dva různé splývají pod stejným názvem, nebo jsou naopak v některých materiálech nadefinované trochu jinak.

Třídění počítáním (counting sort) je jeden z jednoduchých efektivních algoritmů pro třídění n celých čísel, pokud známe jejich maximální rozsah hodnot r (který by neměl být o moc větší, než n). Třídí v čase O(n + r). Jak je obvyklé u algoritmů vnitřního třídění, čísla na vstupu má uložené v poli, do kterého také na konci vytvoří setříděnou posloupnost. Mimo to si tento ale potřebuje pamatovat četnost jednotlivých čísel, proto využívá ještě jedno pomocné pole velikosti rozsahu hodnot r. Bývá to zvykem uvádět tak, že jeho paměťová náročnost je O(r).

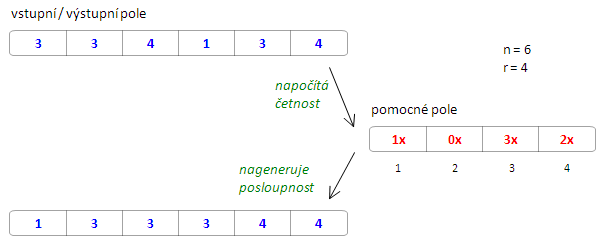
Algoritmus nejdřív naalokuje toto pomocné pole a uloží si do něj samé nuly. Pak postupně prochází vstup a pro každé číslo, na které narazí, zvýší na tomto indexu v pomocném poli hodnotu o 1. Když napočítá četnost všech čísel, postupně prochází pomocné pole a posunuje si index ve vstupním (a zároveň výsledném) poli. Vkládá do něj číslo vždy tolikrát, jaká byla hodnota uvedená v pomocném poli. Podle četnosti tak vlastně od začátku nageneruje novou posloupnost, přepisuje tím původní prvky. Na přiložených obrázcích pro zjednodušení předpokládáme číslování polí od jedničky:

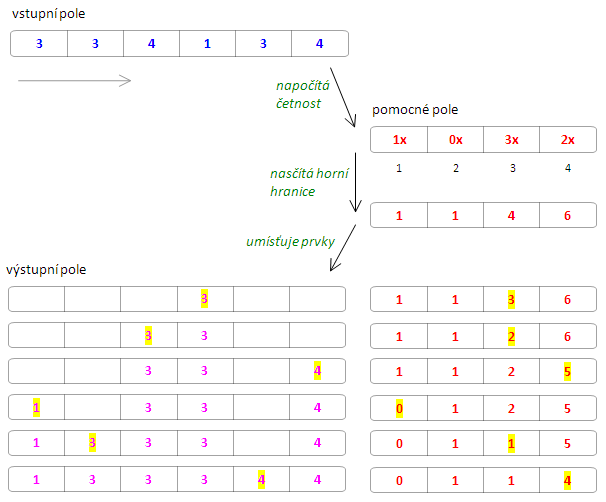
V některé literatuře je pod tímto názvem popisovaná i pokročilejší verze counting sortu, algoritmus poupraví pomocné pole výskytů tak, že ke každé položce přičte počet výskytů předchozích položek. Tím u každé získá přesnou pozici hranice, na které bude toto číslo končit v setříděném poli. Nepřepisuje si vstupní pole, ale pro výstup potřebuje ještě jedno výsledné pole délky n. Prochází vstupní pole, vždy každý prvek umístí na pozici napočítanou v pomocném poli a tuto pozici sníží o 1. Výsledné pole tak zaplňuje jakoby pro každé číslo odzadu.

Přihrádkové třídění (bucket sort)

Co když nepotřebujeme třídit jen celá čísla, ale obecně očíslovanou množinu prvků? Tady už nám nagenerování posloupnosti čísel podle četnosti nebude fungovat, ale můžeme jednoduše využít zmiňovanou pokročilejší verzi counting sortu. Úplně stejně si napočítáme počty prvků označených stejným číslem a opět upravíme toto pomocné pole, aby ukazovalo na místo, kde bude končit poslední prvek s tímto číslem. Potom zase postupně bereme prvky ze vstupního pole, snižujeme pozici napočítanou v pomocném poli a tyto prvky vkládáme do výsledného pole.

Tento algorimus se obvykle nazývá přihrádkové (kbelíkové) třídění, neboli bucket sort. Jak je asi vidět, dokáže setřídit množinu n prvků očíslovaných 1 až r, potřebuje k tomu čas O(n + r) a pamět O(n + r).

Bucket sort má ještě jednu příjemnou vlastnost, po drobné úpravě se jedná o stabilní třídění. To je takové, že každé dva prvky vstupu se stejnou hodnotou klíče jsou na výstupu ve stejném pořadí, jako na vstupu. Můžeme toho jednoduše dosáhnout tak, že při konečném vkládání do výsledného pole procházíme vstupní pole odzadu, tím se nám zachová správné pořadí.

Lexikografické třídění k-tic

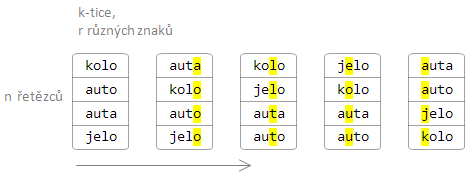
Princip přihrádkového třídění můžeme využít také na řešení dalšího problému. Máme n uspořádaných k-tic prvků, skládajících se z r různých znaků nebo čísel. Úkolem je seřadit tyto k-tice slovníkově (lexikograficky). Můžeme použít metodu rozděl a panuj tak, že prvky setřídíme nejdřív podle první souřadnice k-tic a pak se rekurzivně zavoláme na každou přihrádku a třídíme podle následující souřadnice.

Nebo můžeme využít toho, že bucket sort je stabilní a třídit nejdřív podle k-té souřadnice, pak předposlední atd. až podle první. Že to opravdu platí, se dá dokázat jednoduše matematickou indukcí podle počtu setříděných „sloupečků“. Protože třídí stabilně, prvky se stejnou souřadnicí zůstanou vůči sobě seřazeny stejně, jako v předchozím kroku, a celkové pořadí se nerozhodí.

Časová složitost je O(k * (n + r)), což je lineární s délkou vstupu (k * n) pro pevné k a paměťová složitost je O (n + r).

Radix sort

Pro třídění n celých čísel o maximálním rozsahu r existuje ještě jeden zajímavý algoritmus. Můžeme si zvolit základ Z a čísla zapsat v soustavě o tomto základu. Potom je můžeme lexikograficky setřídit jako k-tice, kde k = dolní celá část log_zr + 1. Pokud bychom zvolili Z = konstanta, časová složitost bude O(log r * n), což může být n * log n, nebo i víc.

Zvolíme-li ale základ rovný délce vstupu Z = n, dostáváme časovou složitost O(log r / log n * n), což pro r ≤ n^α znamená O(α * n). Neboli, pokud je rozmezí čísel polynomiálně velké k velikosti vstupu, lze dosáhnout časové složitosti O(n). Pro neomezeně velký rozsah vstupních čísel se ale Radix sort nehodí. Můžeme ho však použít na cokoliv, co jde vhodně reprezentovat čísly, například tedy i na třídění textu.

Třídění různě dlouhých řetězců

A dostáváme se k závěrečnému problému. Mějme n řetězců r₁, r₂, ..., r_n dlouhých d₁, d₂, ..., d_n. Označme si D jako délku nejdelšího řetězce a R počet znaků abecedy (pozor, předtím jsme počet různých znaků značili malým r).

Pokud chceme třídit obecné řetězce, je problémem jejich rozdílná délka. Když by byly všechny stejně dlouhé, mohli bychom se na ně dívat jako na k-tice, které už třídit umíme. Můžeme se je pokusit doplnit mezerami na stejnou délku a pak setřídit. Tím dostaneme algoritmus, který bude mít časovou složitost O(D * n), což bohužel může být až kvadratické vzhledem k velikosti vstupu. Je to vidět na jednoduchém příkladu: mějme k řetězců, kde prvních k – 1 z nich bude mít délku 1 a poslední řetězec bude dlouhý přesně k. Vstup má tedy délku 2k – 1 a my doplníme prvních k – 1 řetězců mezerami. Vidíme, že algoritmus teď bude pracovat v čase O(k²).

To, co nám nejvíce způsobovalo problémy u předchozího příkladu, bylo velké množství času zabraného porovnáváním doplněných mezer. Můžeme tedy zkusit řešit problém chytřeji a koncové mezery nepřidávat. Nejprve řetězce rozdělíme bucket sortem do přihrádek P_i podle jejich délek, kde i značí délku řetězců v dané přihrádce (jak budeme tyto přihrádky potom v praxi reprezentovat si ještě připomeneme později).

Dále si zavedeme seznam setříděných řetězců S takový, že v něm po k-tém průchodu třídícím cyklem budou řetězce s délkou alespoň D – k + 1 (označme m) a zároveň v něm tyto řetězce budou setříděny lexikograficky od m-tého znaku po D-tý. Z definice tohoto seznamu je patrné, že po D krocích třídícího cyklu bude tento seznam obsahovat všechny řetězce a tyto řetězce v něm budou lexikograficky seřazeny.

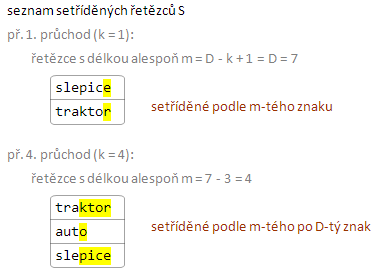
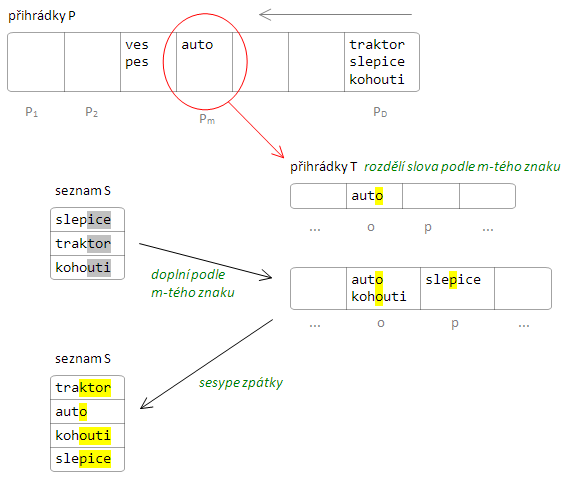
Zbývá už jen popsat, jak tento cyklus pracuje. Nejprve vezme m-tou množinu P_i a její řetězce roztřídí do přihrádek T_j (kde index j značí j-tý znak abecedy) podle jejich m-tého (neboli posledního) znaku. Dále vezme seznam S a jeho řetězce přidá opět podle jejich m-tého znaku do stejných přihrádek T_j za již dříve přidané řetězce z P_m. Tím se zachová, aby delší slovo bylo za tím, co už m-tým znakem končí. Na závěr postupně projde všechny přihrádky T_j a řetězce v nich přesune zpět do seznamu S. Opět si to ukážeme na obrázku, pro přehlednost jsem ještě na vstup přidal jedno slovo (kohouti):

Důkaz algoritmu

Protože řetězce z přihrádek T_j bude brát ve stejném pořadí, v jakém do nich byly umístěny, a protože ze seznamu S, který je setříděný podle (m + 1)-ního znaku po D-tý, bude také brát řetězce postupně, bude seznam S po k-tém průchodu přesně takový, jaký jsme chtěli (setříděný od m-tého znaku).

To si můžeme dokázat matematickou indukcí podle počtu průchodů. Pro k = 1 (neboli m = D) je seznam S zatím prázdný a uspořádáváme řetězce délky D do přihrádek T podle jejich posledního znaku, pomocí bucket sortu. Potom tyto přihrádky T sesypeme postupně do seznamu S. V tom jsou zatím všechny řetězce stejně dlouhé a seřazené podle poslední souřadnice. Po k průchodech již máme prvky setříděny lexikograficky podle m-té až D-té souřadnice a spouštíme (k + 1)-ní průchod, tj. budeme třídit podle (m – 1)-ní souřadnice.

Protože bucket sort třídí stabilně, zůstanou prvky se stejnou (m – 1)-ní souřadnicí vůči sobě seřazeny tak, jak byly na vstupu. Z indukčního předpokladu tam však byly seřazeny lexikograficky podle m-té až D-té souřadnice. Tudíž po (k + 1)-ním průchodu jsou prvky seřazeny podle (m – 1)-ní až k-té souřadnice.

Do přihrádek T vkládáme řetězce ze seznamu S vždy později, z přihrádek P načítáme slova od největších po nejmenší a zpět do seznamu S je také sypeme postupně. Díky stabilnímu třídění se nám tedy pořadí nerozhodí.

Zároveň je z popisu algoritmu jasné, že během třídění každý znak každého řetězce použijeme právě jednou, tudíž algoritmus bude lineární s délkou vstupu. Časová složitost tedy bude O(R * n), kde n je délka vstupu a R počet znaků abecedy. Ještě stojí za připomenutí, že postup bude fungovat jen v případech, kdy má abeceda pevnou velikost.

Schéma algoritmu

Nejdříve si ukážeme schéma algoritmu v pseudokódu a pak si řekneme, jak by se dal v praxi implementovat:

• D ← max(d₁, d₂, …, d_n)   // určí délku nejdelšího řetězce D
• Pro i ← 1 do D opakuj:   // vynuluje pole přihrádek P
  • P_i ← Ø
• Pro i ← 1 do n opakuj:   // podle délek vloží slova do přihrádek P
  • přidej (P_di, r_i)
• S ← Ø   // vynuluje seznam S
• Pro m ← D do 1 opakuj:   // prochází odzadu přihrádky P
  • Pro j ← 1 do R opakuj:   // vždy vynuluje přihrádky T…
    • T_j ← Ø
  • Pro j ← 1 do velikost(P_m) opakuj:  // …a naskládá do nich řetězce z P (podle m-tého znaku)
    • vezmi (P_m, r)
    • pridej (T_r[m], r)
  • Pro j ← 1 do velikost(S) opakuj:  // podle m-tého znaku za ně doplní řetězce ze seznamu S
    • vezmi (S, r)
    • pridej(T_r[m], r)
  • S ← Ø   // seznam S vyprázdní a nasype do něj zpět řetězce z T
  • Pro j ← 1 do R opakuj:
    • Pro k ← 1 do velikost(T_j) opakuj:
      • vezmi (T_j, r)
      • pridej (S, r)
• výsledek S

Reprezentace přihrádek a seznamů, implementace

Je důležité si rozmyslet, jaké budeme mít pro algoritmus vnitřní datové struktury. Přihrádky P a T si můžeme reprezentovat jako běžná pole řetězců velikosti n (počtu všech řetězců na vstupu). Mimo to si k nim ale budeme potřebovat pamatovat, kde ty jejich jednotlivé přihrádky končí. K tomu využijeme druhé pole celých čísel velikosti rozsahu, kam si jejich hranice napočítáme, jako jsme to už dělali u bucket sortu. Ty by měly být v případě přihrádek P indexované maximální délkou slova D a u přihrádek T rozsahem znaků R. Abychom se do toho nezamotali, můžeme si celý tento objekt zabalit do jedné třídy, která si bude pamatovat obě pole i určení minimální a maximální hranice rozsahu. Minimální hranici si pamatujeme proto, abychom mohli indexovat pomocné pole konců přihrádek (P.Bounds) od nuly i v případě, že rozsahem jsou např. číselné hodnoty písmen.

Neuvažujeme vlastně žádné prázdné přihrádky. Řetězce jdou v poli za sebou, kde začínají a končí které přihrádky ukazuje pomocné pole P.Bounds. Přesto nám ale nestačí jít jenom po hranicích v tomto poli (a brát jen zaplněné přihrádky), vypadla by nám některá vkládání ze seznamu S a algoritmus by netřídil podle některých písmen. Proto se vždy pro každý porovnávaný index m podíváme do P.Bounds, jestli pro něj existuje přihrádka, pokud ne, tak prázdnou přeskakujeme a pro tohle m vkládáme jen ze seznamu S.

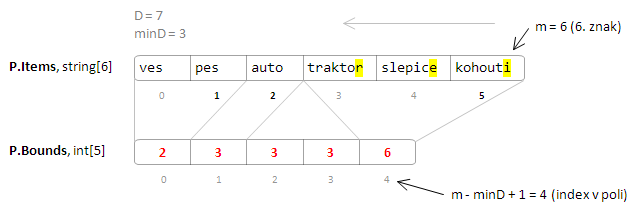
Samotná moje implementace algoritmu se také trochu liší oproti již uvedenému schématu, ale princip zůstává stejný. Rozsahy přihrádek P si napočítáme na začátku a naplníme je prvky. Toto pole potom procházíme od konce, pomocným přihrádkám T vždy nastavíme velikost podle počtu řetězců v dané přihrádce P_m a těch, co už jsou v seznamu S. Aby se zachovalo správné pořadí, jednotlivé přihrádky T zase zaplňujeme odzadu, ale nejdřív do nich doplníme podle m-tého znaku všechny řetězce ze seznamu S (procházíme ho odzadu), potom teprve ty z přihrádky P_m. Když toto dokončíme, tak už máme v poli přihrádek T prvky ve správném pořadí a stačí je pouze přesunout do seznamu S. Ten reprezentujeme obyčejným polem řetězců velikosti n, spolu s informací, kolik je v něm prvků.

Přepočítávání hranic přihrádek T se provádí vždy před přidáváním všech prvků z dané přihrádky P_m a seznamu S už na potřebnou velikost, toto pole se nenatahuje při vkládání každého prvku. Musíme kvůli tomu vždy jen ještě jednou projít přihrádku P_m a seznam S, což nám ale naštěstí nijak nenaruší lineární složitost.

Pro přehlednost a názornost jsem se snažil při implementaci nepoužívat vestavěné kontejnery jako fronty, dynamické seznamy (List<>) apod. Kód jsem naprogramoval v jazyce C#, jako běžnou konzolovou aplikaci pro .NET Framework 3.5. Jediným rozdílem, oproti starším verzím .NET, jsou jenom zkráceně zapsané veřejné vlastnosti ve třídě Buckets. Věřím, že kód by se dal ještě zjednodušit nebo více zoptimalizovat, aby se ušetřilo pár instrukcí procesoru (algoritmus by měl být co nejrychlejší). Asymptoticky by to s ním už ale nepohnulo, proto jsem se spíš držel dosavadního popisu.

Zdrojový kód (C#)

using System;
using System.Collections.Generic;
using System.Text;

namespace StringBucketSort
{
    /// <summary>
    /// Objekt přihrádek; obsahuje pole řetězců, celočíselné pole konců přihrádek a rozsah hodnot znaků
    /// </summary>
    class Buckets
    {
        public int MinValue { get; set; }
        public int MaxValue { get; set; }

        public string[] Items { get; set; }
        public int[] Bounds { get; set; }

        public Buckets(int minValue, int maxValue, int itemsCount)
        {
            MinValue = minValue;
            MaxValue = maxValue;

            Items = new string[itemsCount];
            Bounds = new int[maxValue - minValue + 1];
        }
    }

    class Program
    {
        static void Main(string[] args)
        {
            string[] s = { "ves", "autaky", "traktor", "pes", "autobus", "slepice", "kohouti", "autoatlas", "auto" };

            // Vytiskne nesetříděný a setříděný seznam
            for (int i = 0; i < s.Length; i++)
                Console.WriteLine(s[i]);
            Console.WriteLine();

            s = SortByStringBucket(s, 'a', 'z');

            for (int i = 0; i < s.Length; i++)
                Console.WriteLine(s[i]);
            Console.ReadLine();
        }

        /// <summary>
        /// Přihrádkové třídění textu pro pole stringů, zadává se minimální a maximální znak pro rozsah hodnot
        /// </summary>
        static string[] SortByStringBucket(string[] s, char minChar, char maxChar)
        {
            // Určí délku nejdelšího řetězce D a délku nejkratšího (pro meze přihrádek P); pokud není co třídit, vyskočí ven
            int D = 0, minD = 0;
            int n = s.Length;
            if (s.Length > 0)
            {
                minD = s[0].Length;
                for (int i = 0; i < n; i++)
                {
                    D = Math.Max(s[i].Length, D);
                    minD = Math.Min(s[i].Length, minD);
                }
            }
            else
                return null;

            // Připraví prázdné pole přihrádek P, určí četnost prvků podle délek slov a sečte, kde budou konce přihrádek
            Buckets P = new Buckets(minD, D, n);
            for (int i = 0; i < n; i++)
                P.Bounds[s[i].Length - P.MinValue]++;

            for (int i = 1; i < P.Bounds.Length; i++)
                P.Bounds[i] += P.Bounds[i - 1];

            // Vloží vstup (odzadu) podle délek řetězců do přihrádek P (použije pomocné pole četností, aby si nerozhrabal to původní)
            int[] tempBounds = new int[P.Bounds.Length];
            for (int i = 0; i < P.Bounds.Length; i++)
                tempBounds[i] = P.Bounds[i];

            for (int i = n - 1; i >= 0; i--)
            {
                P.Items[tempBounds[s[i].Length - P.MinValue] - 1] = s[i];
                tempBounds[s[i].Length - P.MinValue]--;
            }

            // Připraví seznam S o velikosti počtu řetězců a objekt přihrádek T
            string[] S = new string[n];
            int sLength = 0;
            Buckets T;

            // Jde podle počtu znaků od nejdelších, rozděluje do přihrádek T podle Pm (pokud v ní něco je) a seznamu S
            for (int m = D - 1; m >= 0; m--)
            {
                T = new Buckets(Convert.ToInt32(minChar), Convert.ToInt32(maxChar), n);

                // Napočítá četnost do přihrádek T, podle m-tého znaku v seznamu S
                for (int i = 0; i < sLength; i++)
                    T.Bounds[S[i][m] - T.MinValue]++;

                // K tomu do T napočítá četnost z přihrádky Pm (pokud existuje), podle m-tého znaku
                // - ověřujeme spodní hranici pole                
                int itemsInBucket = P.Bounds[0];
                if (m - P.MinValue >= -1)
                {
                    if (m - P.MinValue >= 0)
                        itemsInBucket = P.Bounds[m - P.MinValue + 1] - P.Bounds[m - P.MinValue];

                    for (int i = P.Bounds[m - P.MinValue + 1] - 1; i >= P.Bounds[m - P.MinValue + 1] - itemsInBucket; i--)
                        T.Bounds[P.Items[i][m] - T.MinValue]++;
                }
                else
                    itemsInBucket = 0;

                // Sečte, kde budou konce přihrádek T; zkopíruje ho do pomocného pole četností
                for (int i = 1; i < T.Bounds.Length; i++)
                    T.Bounds[i] += T.Bounds[i - 1];

                tempBounds = new int[T.Bounds.Length];
                for (int i = 0; i < T.Bounds.Length; i++)
                    tempBounds[i] = T.Bounds[i];

                // Jde odzadu v seznamu S, rozděluje řetězce podle m-tého znaku do přihrádek T
                for (int i = sLength - 1; i >= 0; i--)
                {
                    T.Items[tempBounds[S[i][m] - T.MinValue] - 1] = S[i];
                    tempBounds[S[i][m] - T.MinValue]--;
                }

                // A stejně tak do přihrádek T přidá i řetězce z přihrádky Pm (pokud ta existuje)
                if (itemsInBucket > 0)
                    for (int i = P.Bounds[m - P.MinValue + 1] - 1; i >= P.Bounds[m - P.MinValue + 1] - itemsInBucket; i--)
                    {
                        T.Items[tempBounds[P.Items[i][m] - T.MinValue] - 1] = P.Items[i];
                        tempBounds[P.Items[i][m] - T.MinValue]--;
                    }

                // Přelije zpět z T do S
                sLength += itemsInBucket;
                for (int i = 0; i < sLength; i++)
                    S[i] = T.Items[i];
            }

            // Vrátí setříděný seznam S
            return S;
        }
    }

}

Závěr

Při psaní tohoto článku jsem vycházel z vlastních materiálů k předmětům Programování I, II a Algoritmy a datové struktury (1. ročník bakalářského studia na MFF UK), z informací na stránkách Martina Mareše http://mj.ucw.cz/ a ze článků na (převážně anglické) Wikipedii, kategorie Sorting algorithm.